HARKEN MUSIC
Harken Music is a new, first-ever mathematical solution for calculating all 1,193,556,233 harmonic combinations and permutations possible in 12-tone music.
Please read the step-by-step description of the math below, and then use the open-source HTML/JavaScript demo at harkenmusic.com to see and hear everything yourself.
Note: A desktop or laptop computer and current web browser (Chrome, Safari, etc.) are required for using the demo; however, there are no downloads, sign-up, or subscription requirements.
Using the demo, you can choose any combination size (from 1 to 12 notes) from the pulldown menu; then select a combination from the numbered list to see and hear all permutations, reflections (inversions), and rotations (transpositions).
Combinations
There are 2,048 possible combinations (n) for each of the 12 potential tonic notes.
In this system, the tonic [0] is fixed and required in every combination—thus we use the binomial coefficient “11 choose n for n = 1 to 11” to calculate the following:
- Tonic (1): 1
- Intervals (2): 11
- Triads (3): 55
- Tetrachords (4): 165
- Pentatonics (5): 330
- Hexatonics (6): 462
- Heptatonics (7): 462
- Octatonics (8): 330
- Nonatonics (9): 165
- Decatonics (10): 55
- Hendecatonics (11): 11
- Chromatic Scale (12): 1
The sum of these results is 2,048, and because any of 12 notes can be used for the fixed tonic [0], the total of all possible unique harmonic combinations is 24,576 (2,048 x 12).
Permutations
When order is considered, the total expands to include 1,193,556,233 possible permutations of 24,576 combinations. Using factorials (n!), we calculate the total number of permutations possible for each combination size as follows:
- 1! = 1 x 1 = 1 tonic
- 2! = 2 x 11 = 22 intervals
- 3! = 6 x 55 = 330 triads
- 4! = 24 x 165 = 3,960 tetrachords
- 5! = 120 x 330 = 39,600 pentatonics
- 6! = 720 x 462 = 332,640 hexatonics
- 7! = 5,040 x 462 = 2,328,480 heptatonics
- 8! = 40,320 x 330 = 13,305,600 octatonics
- 9! = 362,880 x 165 = 59,875,200 nonatonics
- 10! = 3,628,800 x 55 = 199,584,000 decatonics
- 11! = 39,916,800 x 11 = 439,084,800 hendecatonics
- 12! = 479,001,600 x 1 = 479,001,600 tone-rows
Thus the grand sum of all possible unique harmonic combinations and permutations is: 1,193,556,233. The formulas above may be expressed as follows.
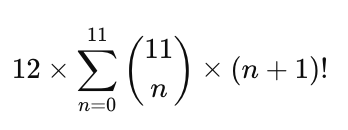
The Numbers
This is a duodecimal or base-12 system that uses the following sequence of 12 unique numbers to identify the notes or pitches in a given combination: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
Any musical pitch may be used for the fixed tonic [0]; and thus every note that follows will be heard relative to the tonic, producing the following intervals.
- [0] = “tonic” or “unison”
- [0, 1] = “minor 2nd”
- [0, 2] = “major 2nd”
- [0, 3] = “minor 3rd”
- [0, 4] = “major 3rd”
- [0, 5] = “perfect 4th”
- [0, 6] = “tritone”
- [0, 7] = “perfect 5th”
- [0, 8] = “minor 6th”
- [0, 9] = “major 6th”
- [0, 10] = “minor 7th”
- [0, 11] = “major 7th”
Unisons and Octaves
We assign unisons and octaves to the same numerical value. For example, the number “0” represents the same pitch class across all octaves, meaning the tonic is “0” whether it’s in the bass, middle, or the treble ranges. While octaves and unisons are technically intervals, they hold no distinct harmonic function beyond emphasizing the foundational tone, serving instead as structural points of return within the tonal space.
We can manage octaves moving in both directions (up and down) using only math. Here’s the formula:
- x = (n + 12y) mod 12
Here’s how it works moving up:
- Set y as a positive integer (e.g., y = 1 moves n up one octave)
Here’s how it works moving down:
- Set y as a negative integer (e.g., y = −1 moves n down one octave)
For example, if we assign MIDI pitch number 50 as the fixed tonic (0) and decide to shift that pitch up one octave (+12), we simply set variables n = 50 and y = 1 and apply the formula, which raises the pitch one octave from MIDI number 50 to 62.
Cycle Order
This system uses two simple formulas to calculate ascending and descending cycles: (n * 7) % 12 for n = 0 to 11 produces the ascending cycle [0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5], while (n * 5) % 12 for n = 0 to 11 produces the descending cycle [0, 5, 10, 3, 8, 1, 6, 11, 4, 9, 2, 7].
Ascending Cycle
(n * 7) % 12 (for n = 0 to 11) = [0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5]
- (0 * 7) % 12 = 0
- (1 * 7) % 12 = 7
- (2 * 7) % 12 = 2
- (3 * 7) % 12 = 9
- (4 * 7) % 12 = 4
- (5 * 7) % 12 = 11
- (6 * 7) % 12 = 6
- (7 * 7) % 12 = 1
- (8 * 7) % 12 = 8
- (9 * 7) % 12 = 3
- (10 * 7) % 12 = 10
- (11 * 7) % 12 = 5
Descending Cycle
(n * 5) % 12 (for n = 0 to 11) = [0, 5, 10, 3, 8, 1, 6, 11, 4, 9, 2, 7]
- (0 * 5) % 12 = 0
- (1 * 5) % 12 = 5
- (2 * 5) % 12 = 10
- (3 * 5) % 12 = 3
- (4 * 5) % 12 = 8
- (5 * 5) % 12 = 1
- (6 * 5) % 12 = 6
- (7 * 5) % 12 = 11
- (8 * 5) % 12 = 4
- (9 * 5) % 12 = 8
- (10 * 5) % 12 = 2
- (11 * 5) % 12 = 7
The cycle order is bi-directional, so ascending and descending cycles may be combined: where the tonic [0] is located in the middle of the sequence, with the tritone [6] at each end.
[6, 1, 8, 3, 10, 5, 0, 7, 2, 9, 4, 11, 6]
The tritone interval [6] appears twice to preserve left-right symmetry, but is only counted once, so the cycle order remains entirely within base-12.
Example
Choosing the four-number combination [0, 4, 7, 10], we calculate (4!) there are a total of 24 possible permutations; a simple recursive function is used to produce the 24 variations in the following order.
- [0, 4, 7, 10]
- [0, 4, 10, 7]
- [0, 7, 4, 10]
- [0, 7, 10, 4]
- [0, 10, 4, 7]
- [0, 10, 7, 4]
- [4, 0, 7, 10]
- [4, 0, 10, 7]
- [4, 7, 0, 10]
- [4, 7, 10, 0]
- [4, 10, 0, 7]
- [4, 10, 7, 0]
- [7, 0, 4, 10]
- [7, 0, 10, 4]
- [7, 4, 0, 10]
- [7, 4, 10, 0]
- [7, 10, 0, 4]
- [7, 10, 4, 0]
- [10, 0, 4, 7]
- [10, 0, 7, 4]
- [10, 4, 0, 7]
- [10, 4, 7, 0]
- [10, 7, 0, 4]
- [10, 7, 4, 0]
Transformations
Reflections (12 Inversions)
Every combination and permutation in music can be transformed (inverted) using reflections. For example, using the 4-number combination [0, 4, 7, 10], we calculate the following inversions using the formula: n_reflected = (2a − n + 12) % 12.
- [2, 0, 5, 8]
- [9, 7, 0, 3]
- [4, 2, 7, 10]
- [11, 9, 2, 5]
- [6, 4, 9, 0]
- [1, 11, 4, 7]
- [8, 6, 11, 2]
- [3, 1, 6, 9]
- [10, 8, 1, 4]
- [5, 3, 8, 11]
- [0, 10, 3, 6]
- [7, 5, 10, 1]
Here’s how it works.
n_reflected = (2a − n + 12) % 12
The expression 2a − n calculates the mirror image of n across the axis a; adding 12 ensures the result remains a positive number, as the subtraction could result in a negative number; the modulo (% 12) limits the range to maintain the 12-tone system.
Example:
To reflect note n = 4 around axis a = 7: compute 2a − n: 2 * 7 − 4 = 14 − 4 = 10; add 12 for safety: 10 + 12 = 22; apply modulo 12: 22 % 12 = 10; so, the reflected note is 10.
Reflection Order = Cycle Order
| No. | Axis | Angle | Cycle |
|---|---|---|---|
| 1 | 0 | 0° | 0 |
| 2 | 3.5 | 105° | 7 |
| 3 | 1 | 30° | 2 |
| 4 | 4.5 | 135° | 9 |
| 5 | 2 | 60° | 4 |
| 6 | 5.5 | 165° | 11 |
| 7 | 3 | 90° | 6 |
| 8 | 0.5 | 15° | 1 |
| 9 | 4 | 120° | 8 |
| 10 | 1.5 | 45° | 3 |
| 11 | 5 | 150° | 10 |
| 12 | 2.5 | 75° | 5 |
Rotations (12 Transpositions)
Every combination and permutation in 12-tone music can be transformed (transposed) mathematically using rotations. For example, using the 4-number combination [0, 4, 7, 10], we calculate the following transpositions using the formula: (n + t ) % 12.
- [0, 4, 7, 10]
- [7, 11, 2, 5]
- [2, 6, 9, 0]
- [9, 1, 4, 7]
- [4, 8, 11, 2]
- [11, 3, 6, 9]
- [6, 10, 1, 4]
- [1, 5, 8, 11]
- [8, 0, 3, 6]
- [3, 7, 10, 1]
- [10, 2, 5, 8]
- [5, 9, 0, 3]
Rotation Order = Cycle Order (Ascending)
Here’s how it works.
(n + t ) % 12, where n = note number and t = transposition; the modulo (% 12) takes the remainder to maintain the 12-tone system.
To rotate any note number or combination, simply add any transposition number; and use modulo to limit range to 12. For example: (n + t ) % 12 = 0 + 7 % 12 = 7. Thus the combination [0, 4, 7, 10] transposes as shown above in ascending cycle order.
Demonstration (Proof of Concept)
Please read the step-by-step description below, and then use the open-source HTML/JavaScript demo* at harkenmusic.com to see and hear everything for yourself.
*Note: a desktop or laptop computer and current web browser (Chrome, Safari, etc.) are required for using the demo; however there are no downloads, sign-up, or subscription requirements.
Using this demo, you can choose any combination size (from 1 to 12 notes) from the pulldown menu; then select a combination from the numbered list to see and hear all permutations, reflections (inversions), and rotations (transpositions).
Conclusion and Discussion
All of 12-tone music is calculable using only this high school-level math.
After exhaustive online research, including extensive prompting of multiple AIs/LLMs, such as ChatGPT4o, Perplexity AI, and Gemini, and consulting with numerous musicians and mathematicians, it appears this system represents a new discovery. The first system ever to use only math to calculate, produce, and play all of the ≈1.2 billion harmonic structures that are possible in 12-tone music.
It cannot be overstated that this new system uses only mathematics and math-related programming code. The programming does not include or use any databases, lookup tables, or other sources of data. Everything—nearly 1.2 billion musical combinations and permutations—is calculated on the fly.
See also: “Harken Music: A New Mathematical Framework for 12-Tone Harmony”, a review by ChatGPT 4o.
Constructive comments, suggestions, and ideas are always welcome here. Persons interested in collaborating, please .
License
© 2024 Mitchell Kahle and Holly J. Huber
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.